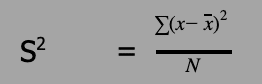MEASURES OF DISPERSION OR VARIATION

This Is the degree to which a group of data varies from their average values.

TYPES OF MEASURES OF DISPERSION:

THE RANGE

Is the difference between the highest and lowest number In a given distribution. For Instance, given the following data: 5,7,4,9,10,6,8 find the range of the above distribution. Now, to get the range, we take the highest number, which is .10 and then minus it from the lowest number, which is 4. Therefore, the range of the distribution is 6, i.e. 10-4 = 6. Or we can simply write the lowest number and the highest number instead of finding the difference. i.e. 4-10.

VARIANCE:

This is the squared deviation of a given set of numbers from their arithmetic mean. It measures the extent to which numerical datas are spread about from their average. The formula is

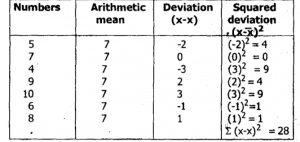
For instance, given the following numbers 5,7,4,9,10,6,8, find the variance of the distribution. To find the variance, first we find the 

arithmetic mean. = (5+7+4+9+10+6+8)/7 = 49/7 = 7

Now to find the variance, we draw a table subtracting the mean from each of the numbers as shown below;

Now, to find the variance from the above table, we divide the squared deviation by the number of items which is 7

i.e. S2  = 28/7 = 4.

THE STANDARD DEVIATION

This is defined as the squared i of the variance and its formula is:

$S=\sqrt{\frac{\sum {\left(x–x\right)}^2}{N}}$

From the distribution given above, we can find the standard deviation (the square root of the variance) by finding the variance, which has already been calculated, and then square it to get the standard deviation. i.e.

$s^2=4$

$s=\sqrt{4}$ = 2

THE MEAN DEVIATION (MD)

This is the arithmetic mean of absolute deviation of the number of a given distribution. The formula is M.D. =(X- X)N

Where x represents variables

X represents the Arithmetic mean

N represents the number of items in a distribution

𝜮 represents the sum of 

In calculating the mean deviation, we make use of absolute value of the deviations. Now, to find the mean deviation taking the distribution given above, we first fInd arithmetic mean, which is already known (7).

M.D = [(5-7) + (7-7) + (4-7) + (9-7)+(10-7)+(6-7)+(18-7)] / 7

 [(-2)+(0)+(-3)+(2)+(3)+(-1)+(1)] / 7

= 1.72 approx.

IMPORTANCE OF MEASURES OF DISPERSION

1. They are very useful for further statistical analysis
2. They are equally useful for extensive income redistribution,
3. They are very useful in stock market accounting and calculations.
4. They are equally useful for industrial quality control.

SIMPLE LINEAR EQUATIONS:

This is the mathematical equation of varying degree. It is the highest power of unknown variables, which determines the degree of an equation. E.g. 3 x + 4 = 2 – equation of first degree with one as the highest power of the unknown value x